
This is the solution for 538's September 20th 2019 Riddler. It is a geometry and trigonometry puzzle. How could I not solve it.
The Simple Problem:
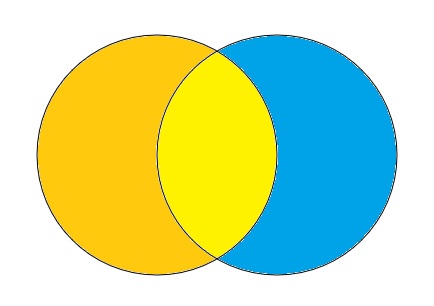
This week, Riddler Nation needs your help designing its new credit card, appropriately named Riddler Express™
The logo consists of two overlapping circles with radius 1 inch, creating three distinct regions: one region that’s shared between the two circles, and two regions that are part of one circle, but not the other.
First need to look at some definitions:
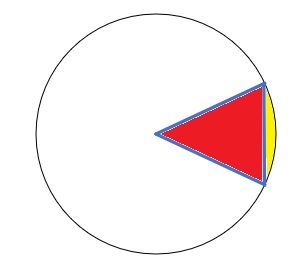
Both the red and yellow shaded areas I'm going to call the slice.
The yellow area is called half of a leaf, the overlapping part of the whole puzzle I'm going to call the leaf.
We need to look at some equations:
Area of a Circle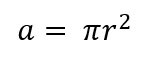 |
Area of a Triangle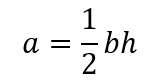 |
Pythagorean Theorem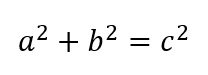 |
Area of a Slice(deg)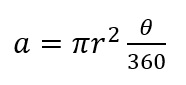 |
Area of a Slice(rad)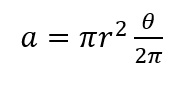 |
Pythagorean Theorem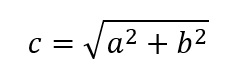 |
Sin to lengths of a triangle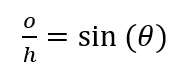 |
Length of the opposite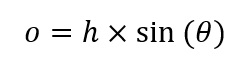 |
OK, my idea was to find the area of the leaf, then subtract it from the area of the circle. This should equal the area of the leaf. To find the area of half a leaf, we take the area of the slice, and subtract the area of the triangle. Then multiply this be two. The nice thing about this puzzle is that all of the radii are 1. This makes the area of the circle π. This also removes the radius from the slice equation. The triangle is a problem.
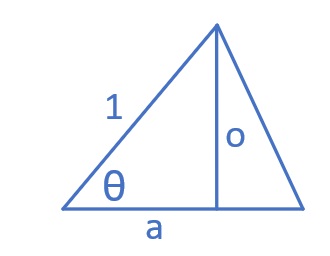
We know both legs are 1, and the θ is the same as the slice. The base can be 1, however the height needs more work, but not much. It's the opposite side to the angle. So all it is, is sin(θ). So half a leaf is:
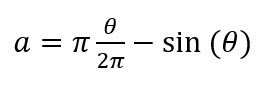
So a full leaf is 2 times that. So the full equation is:
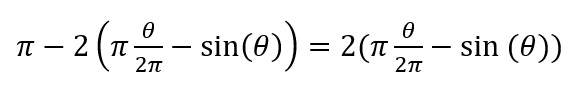
Now we just need to solve for θ.
The problem with this is that it is hard to solve for that. So I wrote a program to spin through the angles
for(double x=132.34645; x < 132.34646; x+=.0000000001)
{
double rad = (x * Math.PI) / 180.0;
double sin = Math.Sin(rad);
double areaTri = sin / 2.0;
double areaSec = (x / 360.0) * Math.PI;
double areaArc = areaSec - areaTri;
double areaCircle = Math.PI;
double area2Arc = areaArc * 2.0;
double areaLeft = areaCircle - area2Arc;
double length = Math.Cos(rad/2.0);
if ((Math.Abs(area2Arc - areaLeft)) < .000000000005)
{
Console.WriteLine(x.ToString() + " " +
area2Arc.ToString() + " " +
areaLeft.ToString() + " " +
(length*2.0).ToString() + " " +
(area2Arc - areaLeft).ToString());
}
}
Once we know the angle, we can use the cos(θ/2) to find half the distance from the center to the middle of the leaf. So two times this is the length to the centers.
The answer is:θ = 132.346458834102 length = 0.807945506598888
The Second part:
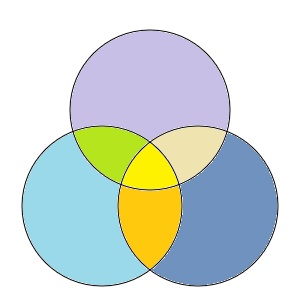
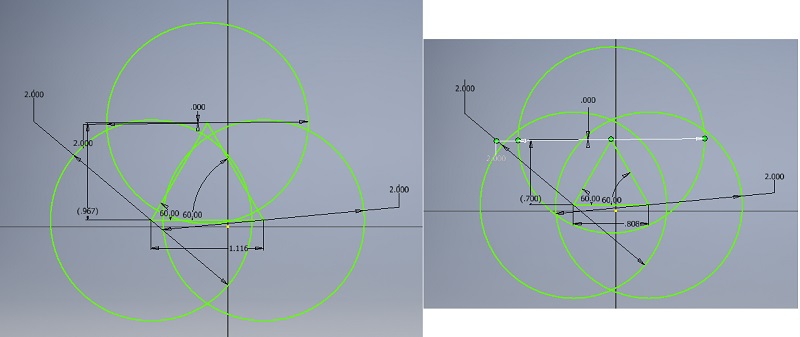
For the second part, we have three triangles, and all of the seven areas have to be equal.
I'm going to start with the equalateral triangle that every point is the center of the unit circle.
The program will change the length of the triangle. The center of the left circle is going to be at (0,0), the center of the right circle is going to be (d,0). And using the 30-60-90 triangle rule, the center of the top circle is:
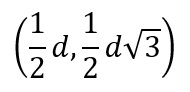
Now, I know how to find the area of a leaf, but we need to find the area of the rounded triangle in the center, and the area of the dart. The area of the dart is the area of the leaf minus the area of the rounded triangle. We need to find this because the left over section of the circles, is going to be the area for the circle minuse the area of the leaf and the area of a dart. To find the area of the leaf we need to find the angle. We are going to use the cosine equation to find half the angle of the of the slice.
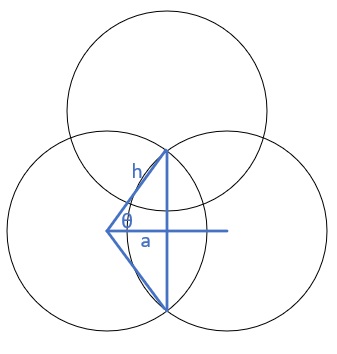
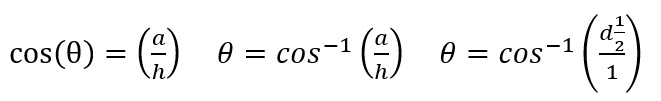
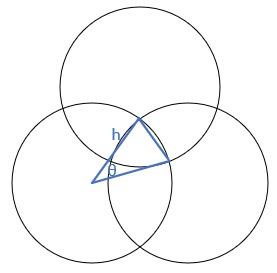
Now we know half the theta, we multiply it by two and we can find the area of the leaf. Now we need the area of the rounded triangle. Notice that the rounded triangle is the area of three half leaves and the area of a triangle. The triangle is tricky it is an equalateral triangle, so finding a side will give us the area. The top point is easy, we can find the top point's y value by using the Pythagorean Theorem:
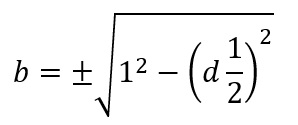
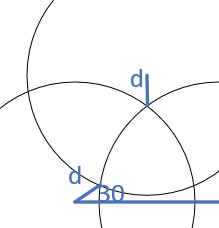
Ok, We know the center of the top circle and the point where the bottom circles intersect. We need to know the distance of these two points, the equation would be hideous, so I'm going to refer to this as dst (distance of the small triagle). The angle of the top line is 30 degrees from the equalateral triangle that forms the distances betweem the circles. Therefore, the bottom left point is 30 degrees from the horizontal line for the bottom circles. So, this point is y = dst*cos(30) and x = dst*sin(30). Once we know the two points we will use the distance formula for the lenth.
Once we know the length of the small triangle, we can figure out the area of the small slice, then the triangle for that slice, and subtracting the two find the area of the small half leaves. We can also figure out the area of the small triangle, then 3 times the small half leaves plus the small triangle will give you the area of the round triangle.
I wrote the program for this however, I learned that I don't quite understand the question. All of the parts never are equal. Either the round triangle matchs the darts:
dist between centers = 1.1160226
Or the round triangle matches the left over circle parts:
dist between centers = 0.8079454
Code:
// Find the area of the leaf
double halfd = d / 2.0;
double halftheta = Math.Acos(halfd);
double theta = halftheta * 2.0;
double sin = Math.Sin(theta);
double areaTri = sin / 2.0;
double areaSec = (theta / (Math.PI*2.0)) * Math.PI;
double areaArc = areaSec - areaTri;
double arealeaf = areaArc * 2.0;
// find the distance of the length of the small triangle in the
// round triangle
double x1 = halfd;
double y1 = Math.Sqrt(1 - halfd * halfd);
double centerTopX = halfd;
double centerTopY = (halfd * Math.Sqrt(3));
double dst = centerTopY - y1;
double x2 = dst * Math.Cos(.5239);
double y2 = dst * Math.Sin(.5239);
double distSideSmallTriangle = Math.Sqrt(Math.Pow(x2 - x1, 2) + Math.Pow(y2 - y1,2));
// Find the area of the small triangle
double t1 = Math.Pow(distSideSmallTriangle, 2);
double t2 = Math.Pow(distSideSmallTriangle / 2, 2);
double heightSmallTriangle = Math.Sqrt(t1-t2);
double areaOfSmallTriangle = (distSideSmallTriangle * heightSmallTriangle) / 2.0;
// Find the area of the slice for the small triangle.
double angleSmallTriangle = Math.Asin(distSideSmallTriangle/2.0) *2.0;
double heightWedgeTriangle = Math.Sqrt(1 - t2);
double areaWedgeTri = (heightWedgeTriangle* distSideSmallTriangle)/2;
double areaWedgeSec = (angleSmallTriangle / (Math.PI * 2.0)) * Math.PI;
// Find the area of the round triangle and the dart
double areaSmallArc = areaWedgeSec - areaWedgeTri;
double areaRoundTriangle = 3 * areaSmallArc + areaOfSmallTriangle;
double areaOfDart = arealeaf - areaRoundTriangle;
// Finally the left over part
double areaLeftOver = Math.PI - (arealeaf + areaOfDart);
if ((Math.Abs(areaOfDart - areaRoundTriangle)) < .0000005)
// if ((Math.Abs(areaRoundTriangle - areaLeftOver)) < .0000005)
{
Console.WriteLine(d.ToString() + " " +
areaRoundTriangle.ToString() + " " +
areaOfDart.ToString() + " " +
(areaRoundTriangle - areaLeftOver).ToString() + " " +
(areaOfDart - areaRoundTriangle).ToString());
}